

A curve of n knots is represented by n - 1 seperate polynomial functions, each with four coefficients it is hardly a data reduction technique. The most common mathematical splines are cubic functions that fit 4 points or 3 points and a first derivative - only the curve between the inner points is used as the generated curve. The technique has expanded to any application where intermediate data points are required.
#Deltagraph stacked plots series#
Spline interpolation, formalized by Newton, uses a series of polynomials to represent the curve of the spline stick given the position of the knots - thus allowing the computation of a smooth ship’s hull to an arbitrary precision using rather crude data as the input. The spline stick was held in place by ‘knots’ or ‘dog’ weights. A spline is simply a bent stick used to generate a curve for drawing the shape of a ship’s hull. If that is not possible one should use the simplest representation that gives an adequate numerical result.įitting polynomials to data points - splining - originated with naval architecture. When fitting a mathematical function to a physical process one should use a function that is derived from the physics of the process. I suspect that the fit is affected to some degree by the number of significant digits shown in Deltagraph's equation display combined with the number of terms and exponentials involved. I've added your raw MGIV at grade 2 data to my python plot and attached it so that folks can see what portion of the curves you're fitting. However, I didn't show out to x=-2.21 for the curves, as your TMY equation peaks near there at about y=1280, which blows the detail because of the extended y-axis. I like to see more of the curve to get a sense of the math and a visual display of what the curve actually describes, even if you're only using a limited portion of the curve to describe film and paper. So the graphs I posted literally use your Deltagraph output, they just cover a wider range than your data, and the peaks are in your equations, just outside the range you use for data. The only change I made was in the power function character, from '^' to the equivalent '**' for python syntax. I literally cut and pasted your two solved equations from post #39 into python and graphed them over the range x=-2 to x=10 in the first graph and over the range x=5 to x=-2 (lower values going right) in the second graph. The curves shown in my graphs are your solutions for TMY and MGIV grade 2, the 'solved' equations you posted in #39 of this thread. Try it, you'll like it (for the toe and linear regions of film curves, not paper)! So, the function that I proposed in the first post to this thread is actually the anti-derivative (integral) of the s-shaped function. So, then I was thinking that what I wanted was a function for which the derivative (gradient) would start at zero, increase over an adjustable range of x values and approach a limiting value, without worrying about the shoulder My original function (the "logistic growth equation") behaves just as I wanted the derivative of a function to behave. In addition, the curve is intrinsically symmetrical, so that the shoulder is basically a reflection of the toe. One limitation is that the width of the toe is not independent of other parameters.

(there was a url link here which no longer exists)Īfter a bit of fooling around with this function, I realized that it probably wasn't all that great for this purpose. The "s-shaped function" described above is actually one that I had suggested in an earlier thread:
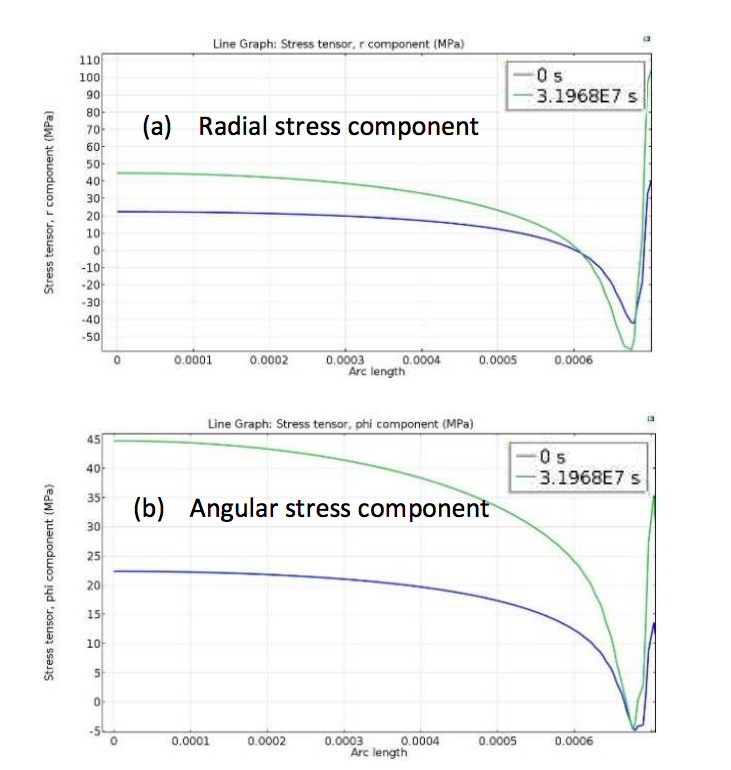
But, that represents a shift of the curve to the right, i.e. To address, Ralph's question yes, an increase in h causes an increase in y for a given x value. It would be interesting to know if this method was actually adopted at Kodak. This obviously requires having very good data for the reference curve. The parameters f, c and h are all relative to the control measurements. In practice, they suggest using for F(x) real, measured data from a film-developer combination that, with the adjustments, can be fit to other data. It is not the same as their F(x), which represents a generic function that can be used to described a family of curves. They discuss the function y = 1/ (1+ e^-x) at the beginning of the paper as an example of a function that looks like a film curve, but that actually doesn't work so well (more about this function, below).
Actually, I don't think that this is what these authors were really doing.


 0 kommentar(er)
0 kommentar(er)
